What may be evident at this point in our Risk-Off series is that for each opportunity we have to make a risk management decision, there is often a corresponding opportunity to make gains within our portfolios.
From taking positions in rallying safe haven currencies to taking the opportunity to be short certain markets, there is often “upside to the downside”.
Touching on risk management in a portfolio from a fixed income point of view, we need to consider that a risk-off environment will be one with lower growth and lower inflation expectations, a scenario where the market (rather than central bank policy) is often in control of the yield curve.
Even if this scenario is not completely in play, in recent years central banks have shown a propensity to guide yields lower than the market would, with no explicit term premium for making a longer-term investment.
However, if our original scenario were to unfold, where yields may drift lower than they even are today where the current market may be pricing in too much inflation:
how can fixed income play a role and where should investors take advantage of the relatively safety within the bond market?
The answer to that lies in the concept of ‘convexity’, and looking beyond the popular investment of today, to seek out longer duration.
Getting Convex
Since this note touches on concepts which can get complex and theoretical, let’s start with the desired outcome and work backwards.
Bonds with long duration and low coupons have greater price sensitivity to interest rate fluctuations, known as “convexity”.
In a risk-off environment, expectations of growth and inflation fall, meaning that long term interest rates would also fall.
If a bond has positive convexity, it will increase in value (price increases) when interest rates fall.
So – if we expect interest rates to fall – then we want to own long duration, low coupon bonds with the strongest positive convexity, with limited to no default probability.
With that laid out, let’s take a step back and define some of these terms.
All the Right Curves
To talk about why we want convexity in a risk-off environment, we need to first touch on a few of the core components that affect a bond’s price and value.
Concept: Duration
Duration is a term that is thrown around a lot but is often misunderstood.
Despite being measured in years, duration is not simply the time until the bond’s maturity date.
Although maturity does influence duration, it is not the only factor.
The three main factors which make up duration are:
- Maturity: the date at which the invested principle is returned
- Coupon: nominal yield or income paid out by the bond, relative to bond’s par value
- Yield to Maturity: the total return that will be paid out by the maturity date, based upon the bond’s current market price
All of this results in duration, a measure of how fluctuations in interest rates will affect the price of a bond.
Higher/longer duration indicates that the bond’s price will move strongly in the reverse direction of interest rates, whereas low duration has low sensitivity to interest rate movements or may just move in direct proportion.
As an example:
Prior the interest rate volatility that we saw in February/March, we recommended clients maintain short duration within their portfolio, which would preserve value and dampen volatility amid fears of rising yields/rates.
The maths is simple; if rates were to rise 1%, then a bond with 1-year duration would lose ~1% of its value, but a bond with 10-year duration would lose ~10% of its value (ceteris paribus).
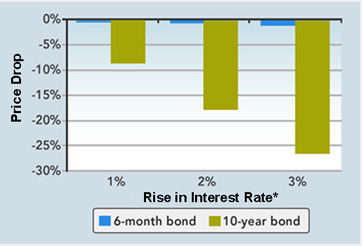
Source: Fidelity
But this also goes the other way, and bonds with long durations also gain value (in magnitudes more than short duration) if yields/interest rates fall.
Concept: Convexity
We now know that duration measures the change in price due to a movement in interest rates.
But how much will duration change relative to interest rates?
Convexity, in mathematical terms, is the first derivative of duration: convexity measures how sensitive the duration of a bond is to a change in yield/rates.
This makes convexity one of the most important risk metrics we can consider for a fixed income portfolio, and also introduces “curvature” into bond investing. Let’s see a graph:
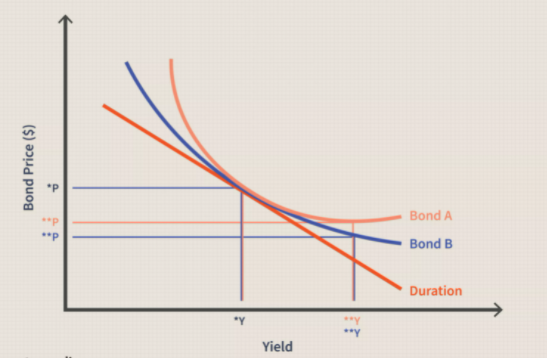
Source: Investopedia
The orange line shows the duration of any given set of bonds as a relationship between bond price and bond yields.
As yields (interest rates) fall, bond prices rise, and vice versa. Duration measures the sensitivity of price to this change in yield. Convexity then measures the sensitivity of duration to changes in yield.
The light orange coloured line is the convexity of Bond A.
If you look at Bond A on the graph, as the price falls, the yield of Bond A increases – but this occurs at a decreasing rate the more price falls.
The curvature of the convexity line represents the difference between the actual price at the time of price fluctuation, and what the straight duration line says it would be at a given point.
The Long (Duration) Shot
Now that we understand the components of our ideal outcome, let’s come back to the investment idea: buying long duration bonds.
In a risk-off environment, we have historically seen bonds rally (price goes up, yield goes down).
Given this environment, lets us pick which part of the yield curve (i.e. how long duration) will give us the most growth for any given fall in interest rates.
Take a look at the distribution of duration across different U.S Treasuries:
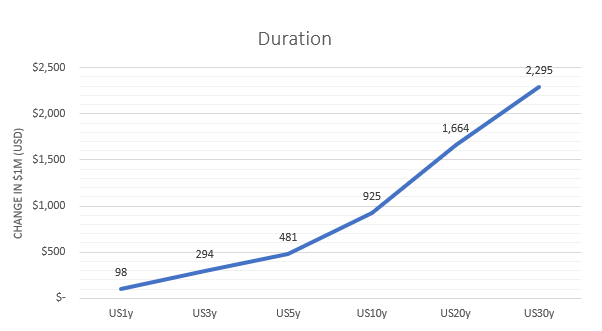
Source: Mason Stevens
Keeping a constant investment of a hypothetical $1 million USD, the distribution shows the difference a one basis point change in yield would make to your investment across different U.S. Treasuries.
The difference in value between a 1 year and 30-year treasury is over 23x. This is because the US30s have a greater positive convexity, their duration is more sensitive to changes in yields.
And in the event of risk-off markets, the greatest positivity convexity is where an investor would find the greatest absolute value across the fixed income yield curve.
In terms of investible vehicles, there are several ETFs which focus on exposure to the long end of the yield curve. One of the largest and longest running is the iShares 20+ Year Treasury Bond ETF (TLT:NASDAQ), which tracks the index of U.S Treasury Bonds out past 20-year maturity dates.
In the below chart, the ETF did quite well during the 2020 pandemic, where bonds rallied (yields dropped)
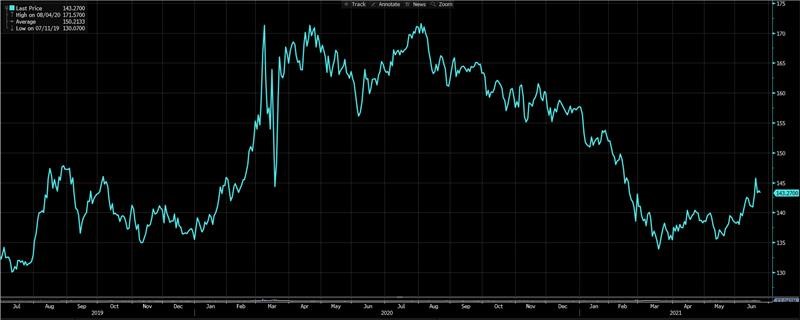
Source: Bloomberg
In terms of getting a direct, tailored exposure to convexity, Mason Stevens are Fixed Income Specialists and have a long track record of constructing tailored solutions for clients seeking particular strategies within the bond market.
We are always happy to assist in building a direct bond portfolio, and also to assist with fund selection too.
Out to the Future
As with other ideas in this series, in times where certain markets are falling, there are almost always ways to protect or enhance a portfolio.
In a risk-off circumstance, investors may be tempted to flee to fixed income as a protection/diversification away from equity risk premia and associated capital losses.
Finding solace in long duration, high convexity bonds may operate as more than just diversification, but as a hedge to find returns.
It sounds a far cry from the current landscape, where markets fear rising interest rates, but if there’s a single defining point to this series, it is to be prepared for what the market thinks will never happen.
The views expressed in this article are the views of the stated author as at the date published and are subject to change based on markets and other conditions. Past performance is not a reliable indicator of future performance. Mason Stevens is only providing general advice in providing this information. You should consider this information, along with all your other investments and strategies when assessing the appropriateness of the information to your individual circumstances. Mason Stevens and its associates and their respective directors and other staff each declare that they may hold interests in securities and/or earn fees or other benefits from transactions arising as a result of information contained in this article.



